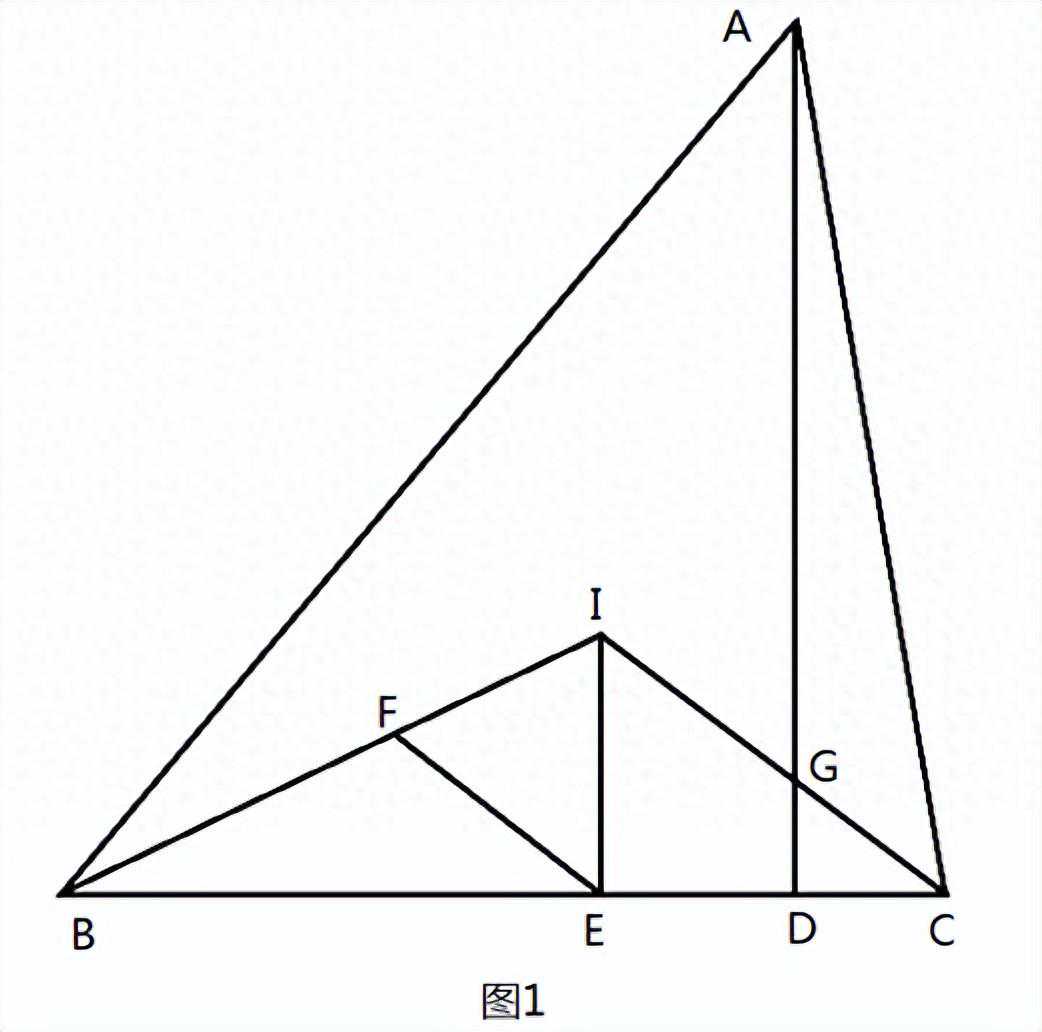
题目1:如图1,I为△ABC的内心,IE⊥BC于E,AD⊥BC于D,F为BI上一点,EF=EI,CI、AD交于G。求证:F、I、G、D四点共圆。
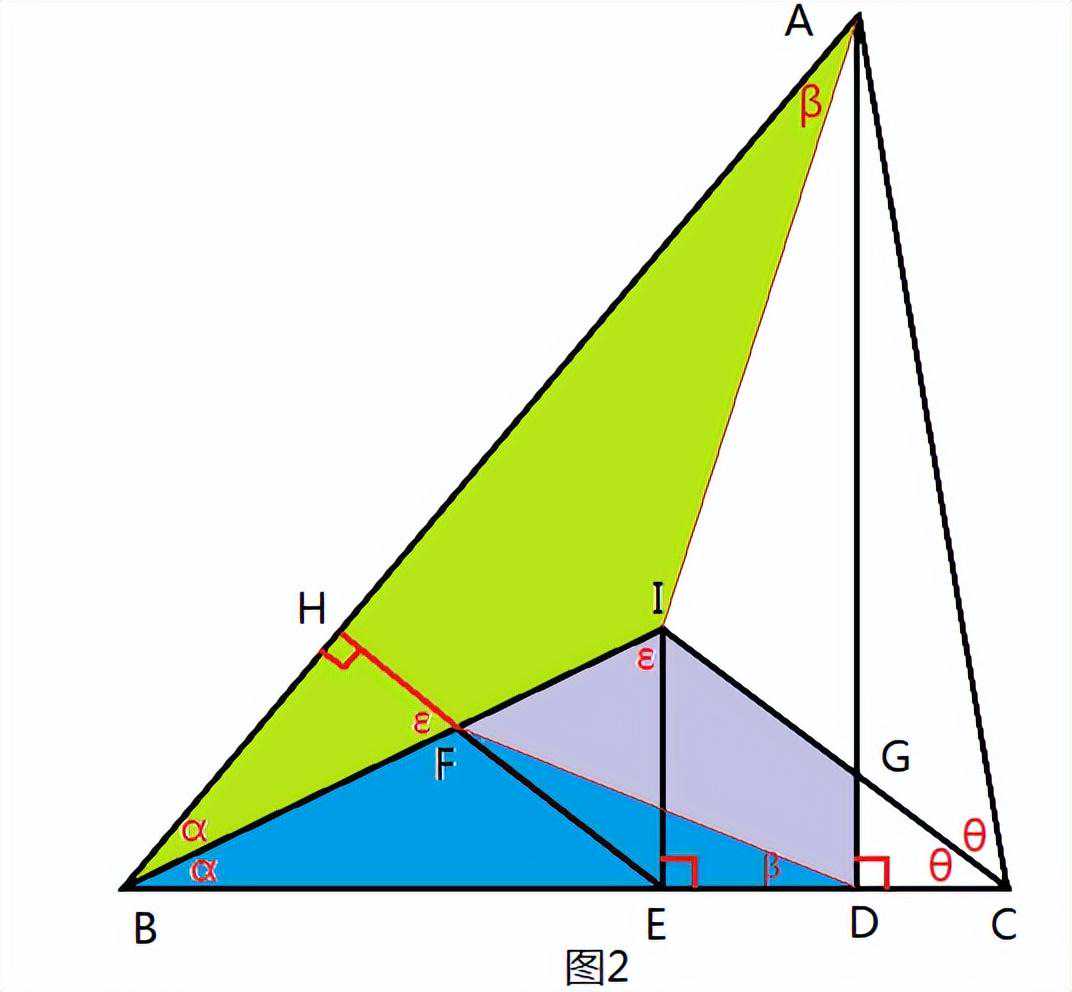
解题思路:延长EF交AB于H,连接FD、IA(图2)。
易证△BHF为Rt△,则Rt△BEI∽Rt△BHF,
BE/BH=BI/BF;
易证Rt△ABD∽Rt△EBH,则BE/BH=AB/BD。
故BI/BF=AB/BD,即AB/BI=BD/BF,
结合∠ABI=∠DBF=α,则△ABI∽△DBF,
故∠BDF=∠BAI=1/2∠BAC。
已知∠BDF=90°-∠FDA,则∠FDA=90°-1/2∠BAC。
在四边形FIGD中,
∠FIG+∠FDG
=∠BIC+∠FDA
=(90°+1/2∠BAC)+(90°-1/2∠BAC)
=180°,故F、I、G、D四点共圆成立。
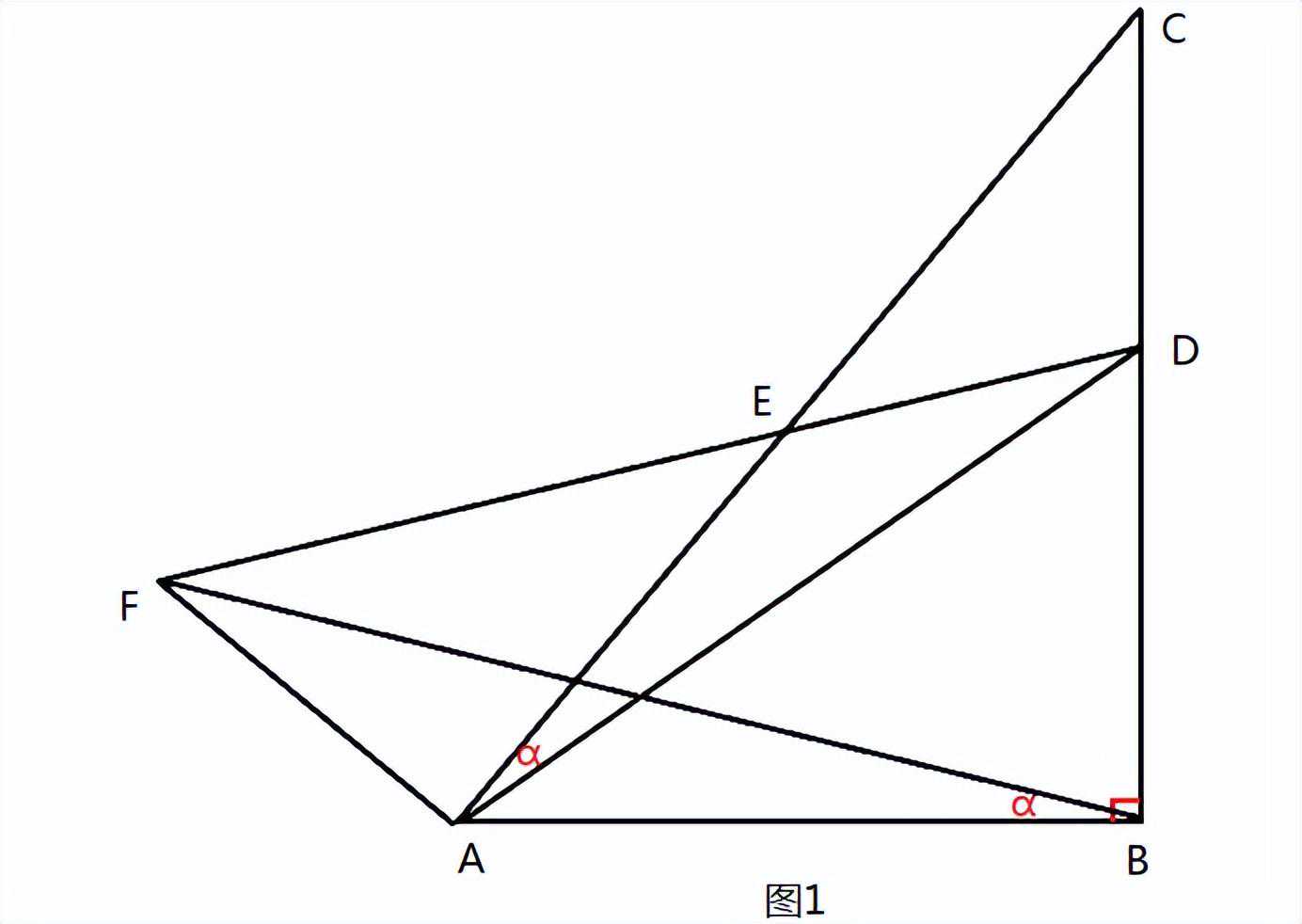
题目2:如图1,在△ABC中,∠ABC=90°,点E是AC的中点,∠CAD=∠ABF。求证:FA⊥AC。
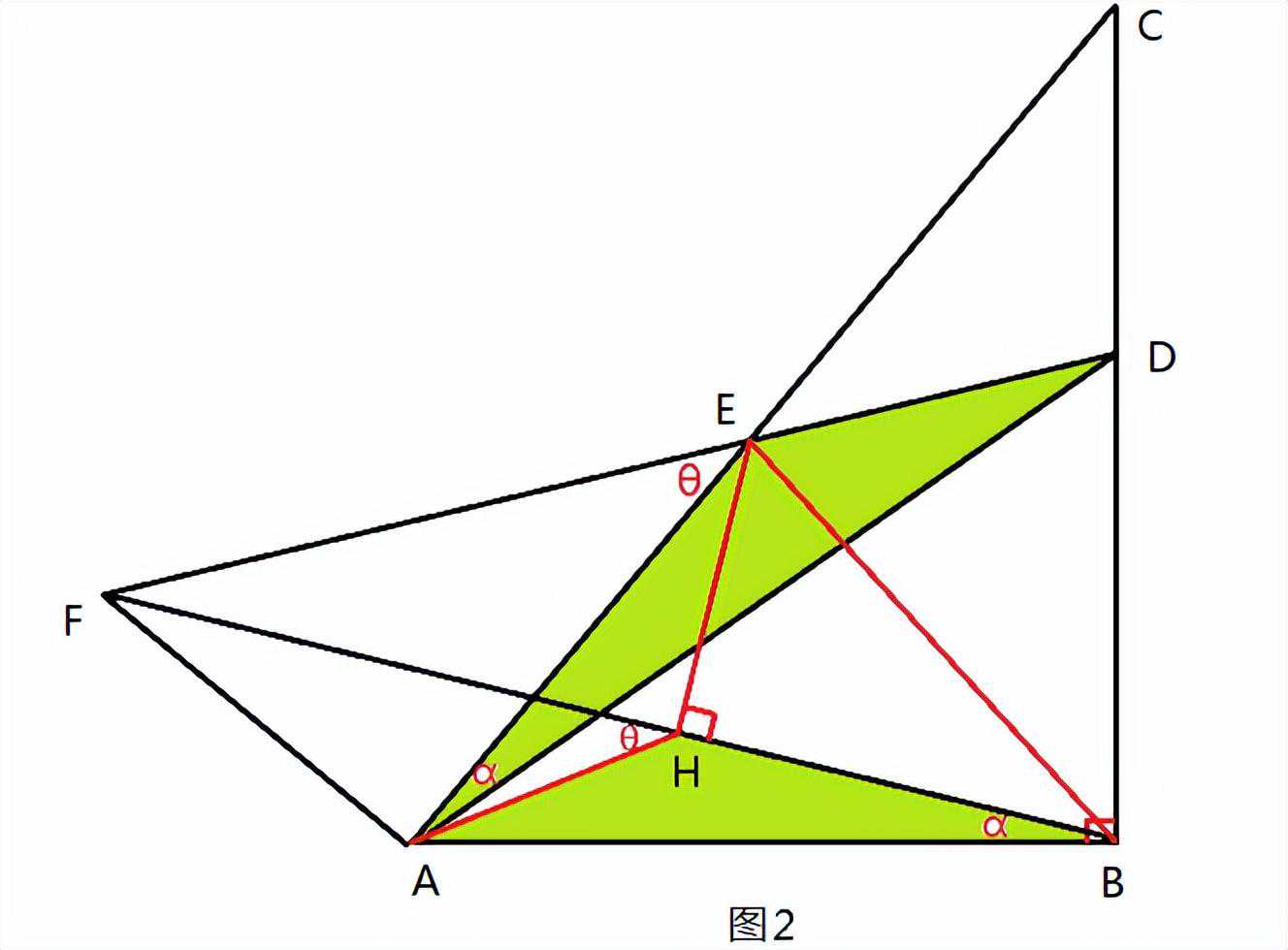
解题思路:作EH⊥FB于H,连接EB、HA(图2),则EA=EB。
易证∠EBH=∠DAB,则Rt△ABD∽Rt△BHE,
故AB/HB=AD/EB=AD/EA,已知∠CAD=ABF,
则△AHB∽△DEA,∠AHB=∠DEA,
∠FHA=∠FEA=θ(等角的补角相等),
E、F、A、H四点共圆成立,
∠FAE=∠FHE=90°,
FA⊥AC得证。
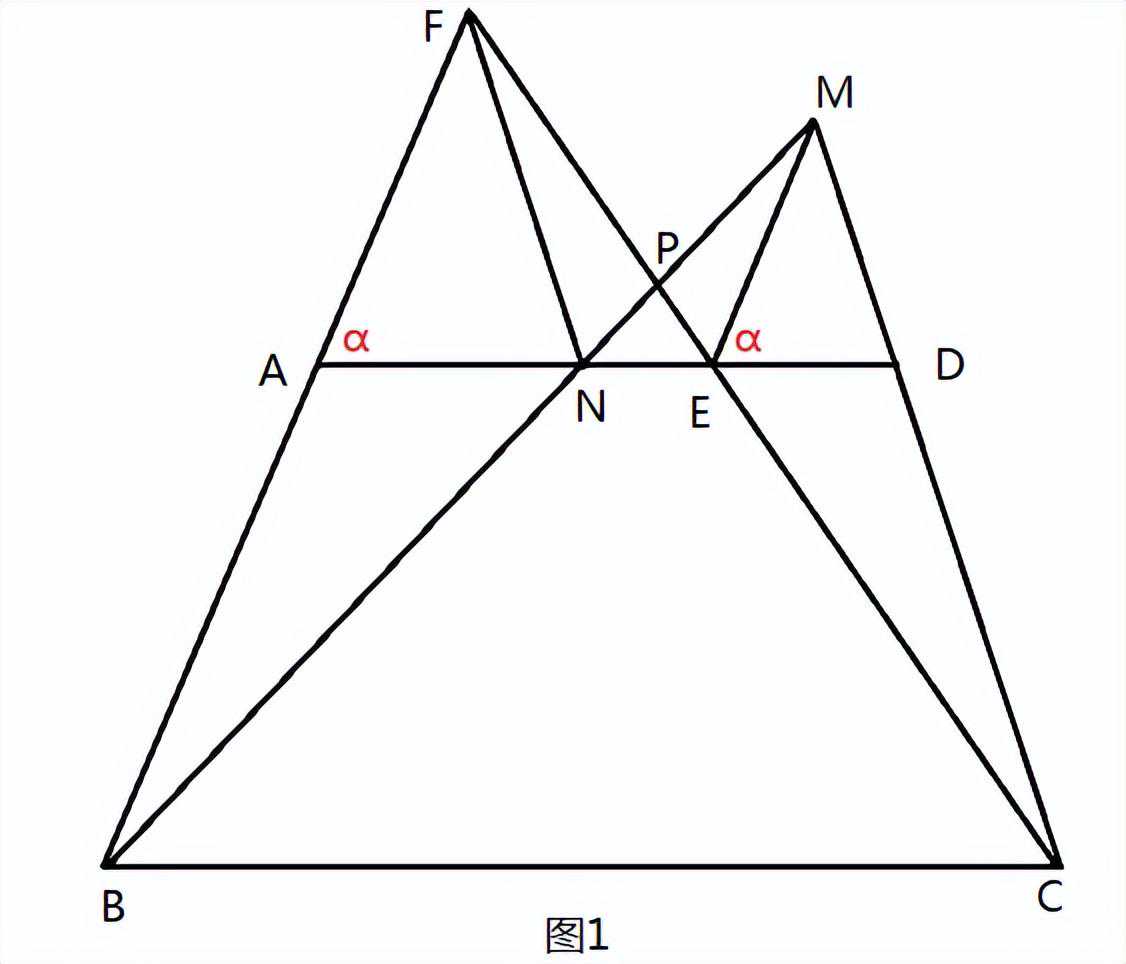
题目3:如图1,在梯形ABCD中,AD∥BC,E在AD上,CE的延长线交BA的延长线于F,过点E作AB的平行线交CD的延长线于点M,BM与AD交于点N,BM、CF交于点P。求证:FN∥MC。
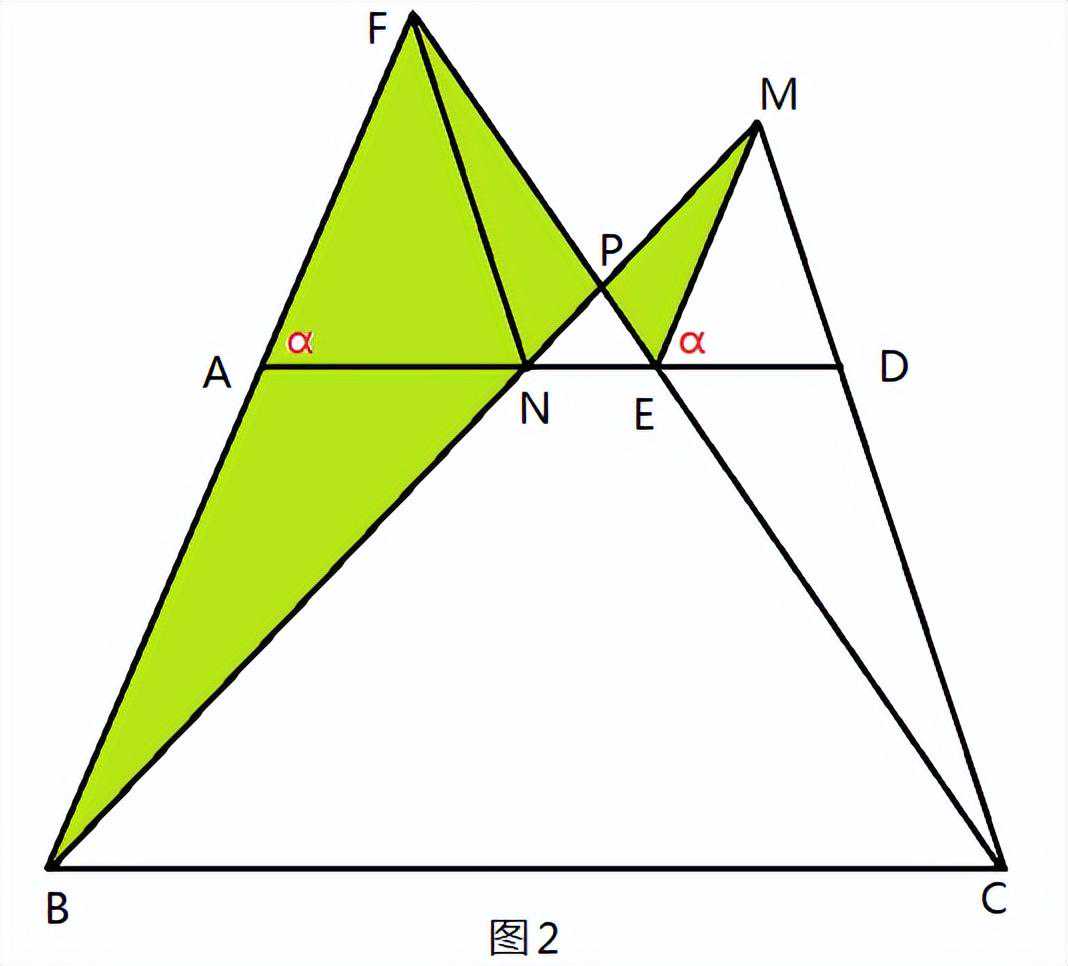
解题思路:已知EM∥BF,则△PBF∽△PME(图2),
PB/PM=PF/PE,即PB·PE=PM·PF。
易证△PNE∽△PBC(图3),PN/PB=PE/PC,
即PB·PE=PN·PC。

则PM·PF=PN·PC,即PF/PN=PC/PM,
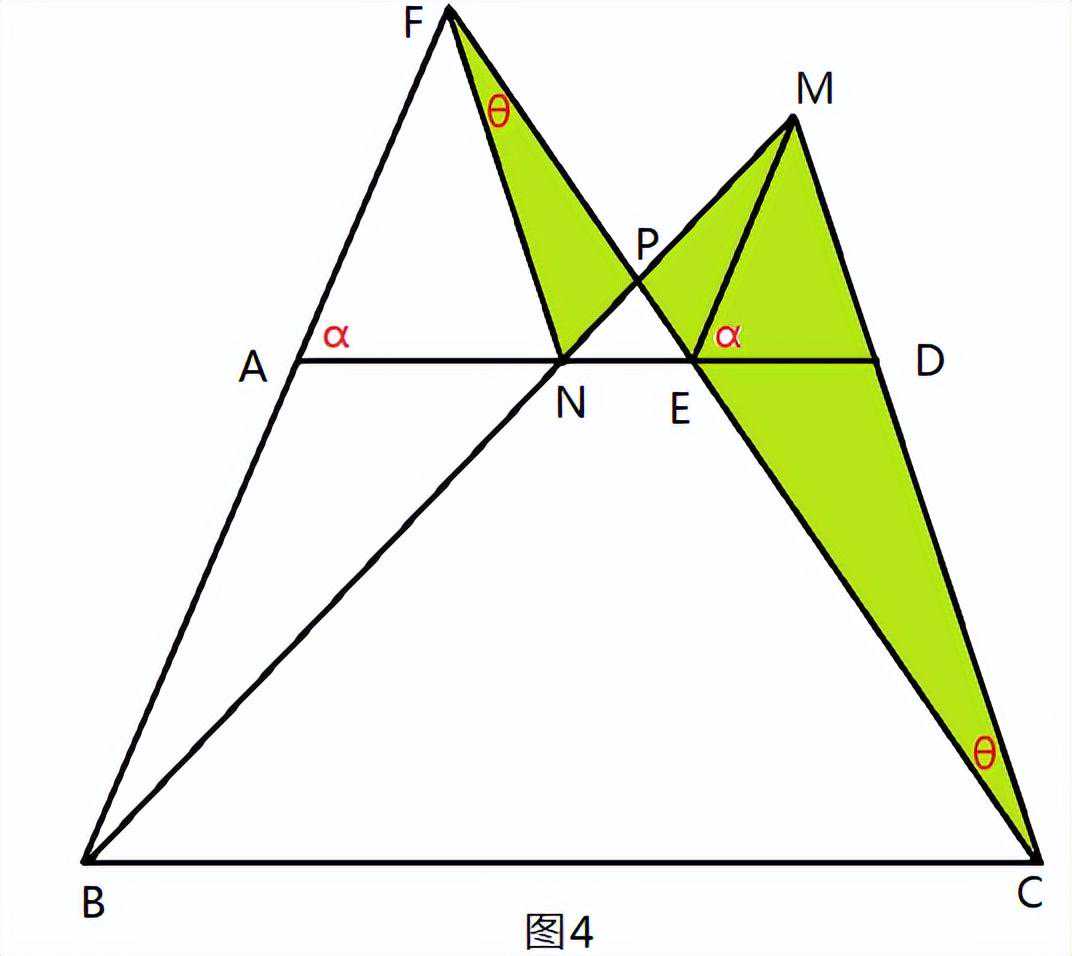
结合∠FPN=∠CPM,则△FPN∽△CPM(图4),
故∠PFN=∠PCM,FN∥MC成立。
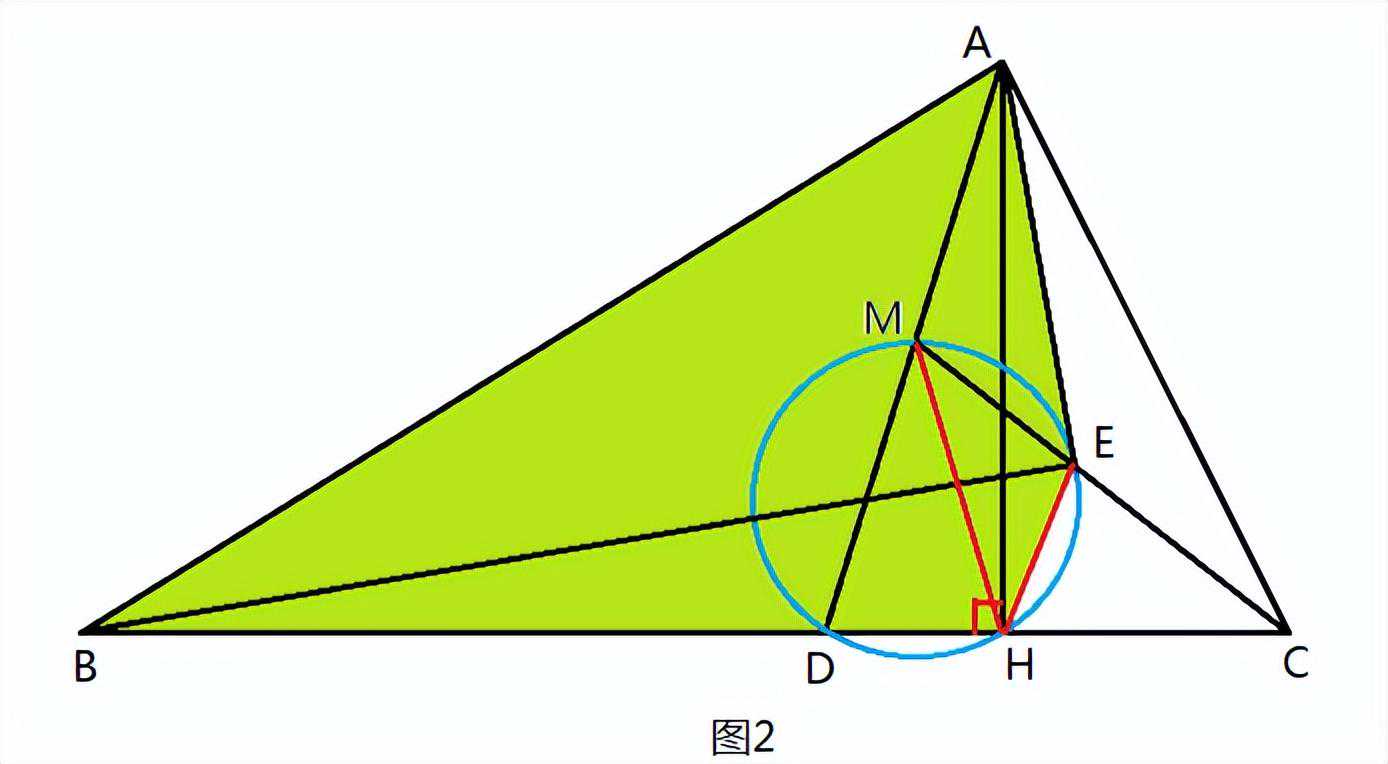
题目4:如图1,AD、AH分别是△ABC(AB>AC)的角平分线和高线,M是AD的中点,△MDH的外接圆与CM交于点E。证明:∠AEB=90°。

解题思路:已知AH⊥BC,Rt△AHB与△AEB有共边AB,如A、B、H、E四点共圆,则可证明∠AEB=90°。
连接MH、EH(图2)。
已知M为Rt△ADH斜边上的中点,故MA=MD=MH,
∠MDH=∠MHD;
又知AD为∠BAC平分线,则∠BAD=∠CAD。
因四边形MDHE为圆内接四边形,∠CHE=∠DME,
∠MDH+∠MEH=180°,即∠MHD+∠MEH=180°,
而∠MHD+∠MHC=180°,故∠MHC=∠MEH。
易证△MHC∽△MEH(母子相似三角形),
则有MH²=ME·MC,即
MA²=ME·MC。
在△AME和△CMA中,
∠AME=∠CMA,MA/ME=MC/MA,
则△AME∽△CMA,∠MAE=∠MCA。
在四边形BHEA中,
∠BHE+∠BAE=∠BHE+(∠BAD+∠MAE)
=∠BHE+(∠CAD+∠MCA)
=∠BHE+∠DMC
=∠BHE+∠CHE
=180°,故A、B、H、E四点共圆,
∠AEB=∠AHB=90°。