研究背景
计算方法
本文使用量子ESPRESSO发行版中的PWscf包实现的密度泛函理论(DFT)进行理论计算。考虑了广义梯度近似(GGA)内的Perdew–Burke–Ernzerhof(PBE)泛函来描述交换和相关效应。使用PAW赝势来处理核心电子,平面波基组的截断能为450eV。对于一维ZGNR和AGNR模型结构,通过1×7×1和1×15×1K点网格分别获得了Brillouin区域内的Monkhorst-Pack方案。通过考虑15Å的真空,避免了重复图像之间的相互作用。能量和力分别收敛在每个原子0.001meV和0.01eV/Å的阈值标准内。
结果与讨论
石墨烯纳米带(GNR)是适合掺杂更大尺寸杂原子(如硫和磷)在边缘上,从而诱导出大量活性碳位点的合适候选者。根据边缘,GNR主要分为两种类型:锯齿纳米带(2n-ZGNR)和椅子型纳米带(n-AGNR),表现出不同的特性,其中n表示纳米带的宽度。在ZGNR和AGNR的边缘处,碳原子使用氢原子被占据。首先,考虑了6-ZGNR和11-AGNR模型,通过13种不同的硫(S)、磷(P)、二氧化硫(SO2)和二氧化磷(PO2)的配置进行边缘掺杂(图1,S1)。掺杂配置如下:S、SO2、P、PO2、2S、2P、2SO2、SP、SSO2、SPO2、PSO2、PPO2、SO2PO2。对于GNR模型中的每种边缘掺杂配置,同时确定了一些碳位点作为可能的ORR活性位点(图1)。最终通过ZGNR和AGNR中各种边缘掺杂配置设计了共计136种不同的活性位点(26个系统)。
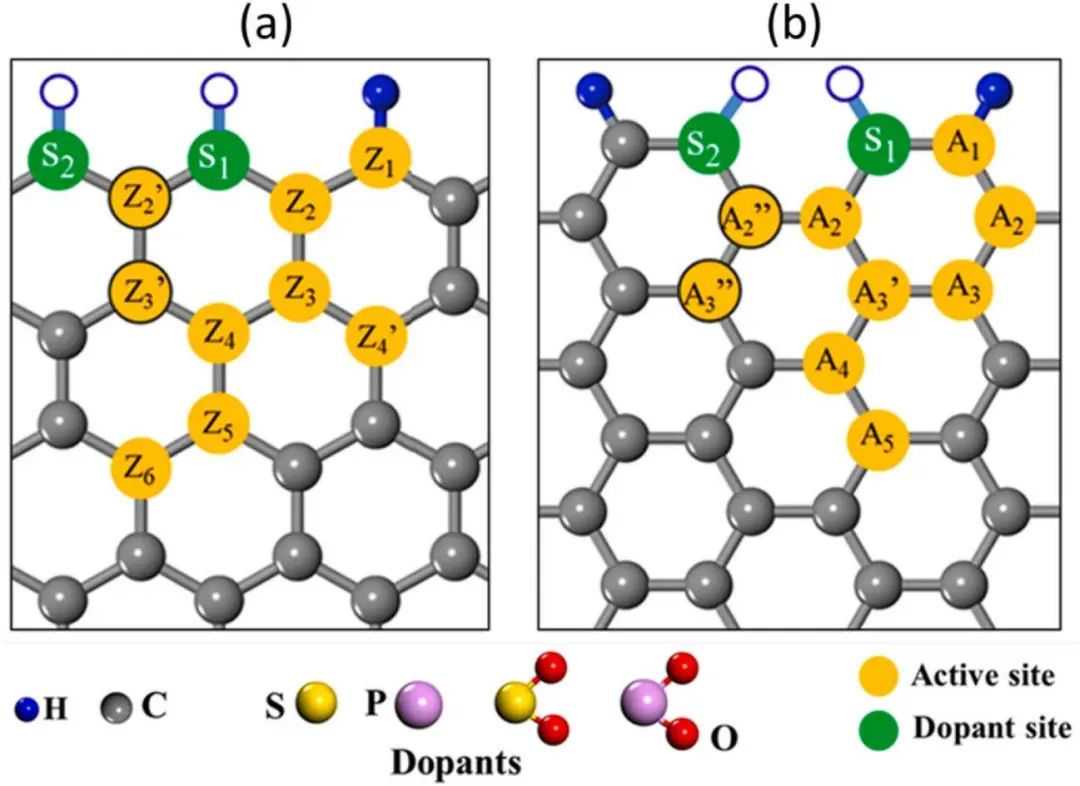
图1GNR催化剂掺杂结构
对所有这些136个位点(总共408个DFT计算)上的三种主要中间体O*、OH和OOH进行了碱性ORR计算,并用于绘制自由能曲线。在图2a中,展示了在不同外加电位(U=0V,0.4V,-0.29V,-0.83V)下,2S掺杂6-ZGNR的Z3位ORR自由能(记为Z3_2S@6-ZGNR,其他模型体系也使用类似的符号)。从平衡势(U=0.4V)下的自由能可以看出OOH*中间产物形成的第一步的η值为0.69V。所以对于U=−0.29V,ORR整体过程均为放热反应。因此,ΔGOOH和ΔGOH都可以用作预测ORR活动的能量描述符,而且它们与R2的线性关系为0.96。在这里,作者进一步的研究中考虑了ΔGOH作为一个能量描述符。绘制了ηvsΔGOH的曲线,并发现它们之间有着火山类型相关性。利用ΔGOH与Dπ(EF)和R-Oπ的简单线性拟合方法,得到的R2(拟合优度)分别为0.67和0.66。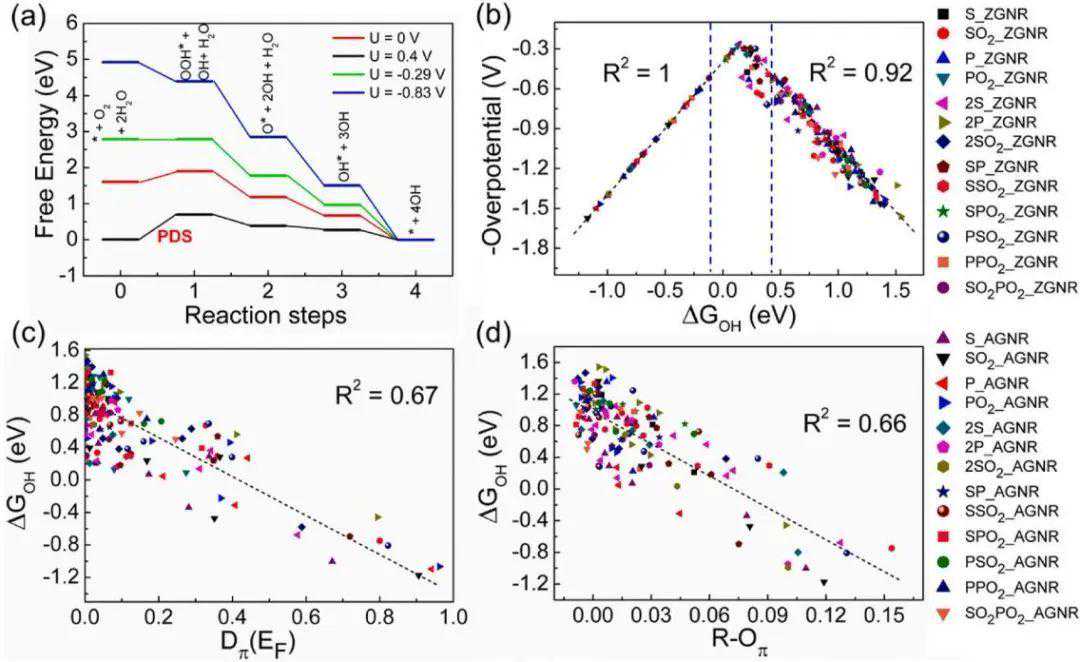
图2析氢自由能和特征值间的线性拟合
在图3中,展示了宽度依赖性分析,以揭示ZGNR和AGNR的ΔGOH和π轨道描述符之间的确切关系。可以看到,ΔGOH的值作为ZGNR宽度的函数呈指数增长(图3a)。而Dπ(EF)和R-Oπ值作为ZGNR宽度的函数呈指数下降(图4b-c)。另一方面,通过增加AGNR的宽度,ΔGOH、Dπ(EF)和R-Oπ的值在阻尼正弦波形中变化(图4d-f)。该AGNR波形与三个宽度族(3n,3n+1,3n+2)相关,其中上述参数随特定宽度族的变化呈指数行为。从这个宽度相关的研究中,可以推断,Dπ(EF)和R-Oπ与能量参数并不遵循精确的线性关系(ΔGOH)。但是ΔGOH和π电子描述子之间的关系可以是非线性的,ΔGOH应该与Dπ(EF)和R-Oπ的特殊函数相关联。
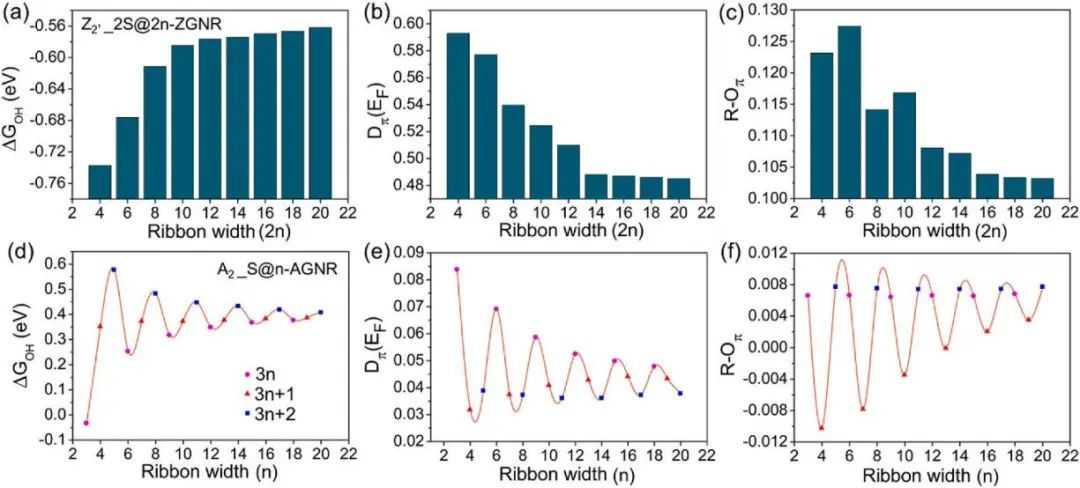
图3ΔGOH与Dπ(EF)和R-Oπ的线性关系
为了更好地实现ΔGOH和π电子描述符之间的相关性,本文应用了各种机器学习(ML)算法,可以捕获特征和输出之间的非线性。使用了六种类型的ML回归算法[多元线性(MLR)、决策树(DTR)、随机森林(RFR)、支持向量机(SVR)、最近邻(KNN)、极端梯度增强(XGB)],这些算法在处理数据集时具有不同的工作原理。将DFT计算的161个数据点(包括图4的值)分成80%用于训练,20%用于测试ML模型。在这里,Dπ(EF)和R-Oπ的值作为描述符/特征,ΔGOH是ML算法的输出。通过调整训练数据集的超参数并评估其在测试数据上的性能,建立了六个预测模型。
在ML研究中,kfold交叉验证是一项重要的技术,它利用不同的训练/测试集来分析给定数据点的过拟合或选择偏差等问题。在这里使用5折交叉验证方法,使用重复采样技术来筛选ML模型的准确预测能力。在图5中,绘制了使用DFT计算的ΔGOH与使用各种ML预测模型对测试数据估计的ΔGOH的图。通过5折交叉验证方法,我们得到了测试数据集对ML模型的拟合优度(R2),其排序为:SVR(0.87)KNN(0.84)MLR(0.84)RFR(0.83)XGB(0.79)DTR(0.78)。同时应用Eqn(4)对测试数据点的ΔGOH值进行估计,其R2为0.79。
有趣的是,SVR模型被认为是最优的预测模型,具有较高的拟合优度(R2)。径向函数(RBF)可以有效评估非线性数据集而闻名,基于RBF的SVR预测模型可以检测到ΔGOH与π轨道描述子之间相关性的非线性较小,这是其预测性能较高的原因。
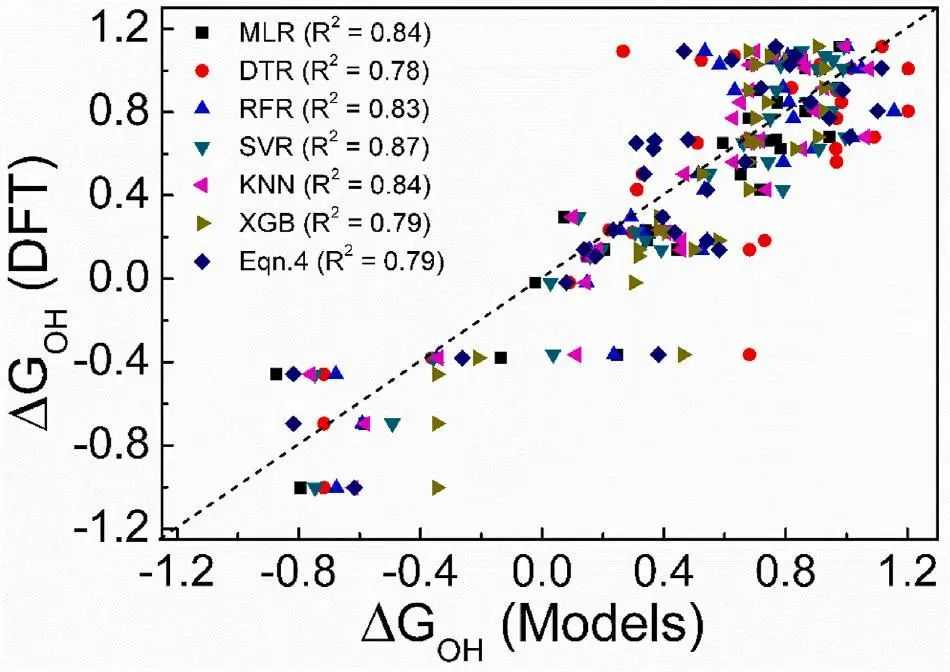
图4机器学习预测特征关联
进一步探讨能量和电子描述符与纳米带宽度的关系,见图5。这种方法可以帮助我们预测不同宽度的新GNR催化剂的活性,而无需进行DFT计算。这表明,扶手椅纳米带显示由三个不同宽度家族(3n,3n+1,3n+2)相关的阻尼正弦波,其中每个家族都由指数曲线表征。在这里,这种结构关系是通过绘制S@AGNR在所有宽度上的六个不同活性位点(A1,A1',A2,A2',A2'',A3)的Dπ(EF)值来探索的(图5a)。可以观察到,每个活动位点的波形具有特定的振幅(A)和平均值(y0)。有趣的是,A和y0之间也存在线性相关(图5b)。如图5c所示,该阻尼正弦曲线可以分解为三个指数波,每个指数波对应一个特定的宽度族。利用这种结构相关性,本文演示了用最小DFT计算估计不同宽度的Dπ(EF),R-Oπ和ΔGOH值的新方法。
随着条带宽度的增加,数值逐渐接近平均值(y0),宽度的最后三个点(如18、19和20-AGNR)最接近y0。作者使用18、19和20-AGNR的平均Dπ(EF)来估计y0值,而3、4和5-AGNR的值作为指数曲线的起点,并用于寻找振幅“A”。剩余宽度的Dπ(EF)值可以通过绘制基于这6个点的指数曲线。图5d显示了Dπ(EF)值与DFT计算值的比较,R2为0.99。同样,只需要6个DFT计算的R-Oπ值(如图S7所示),就可以映射出三个带宽下的条指数曲线。
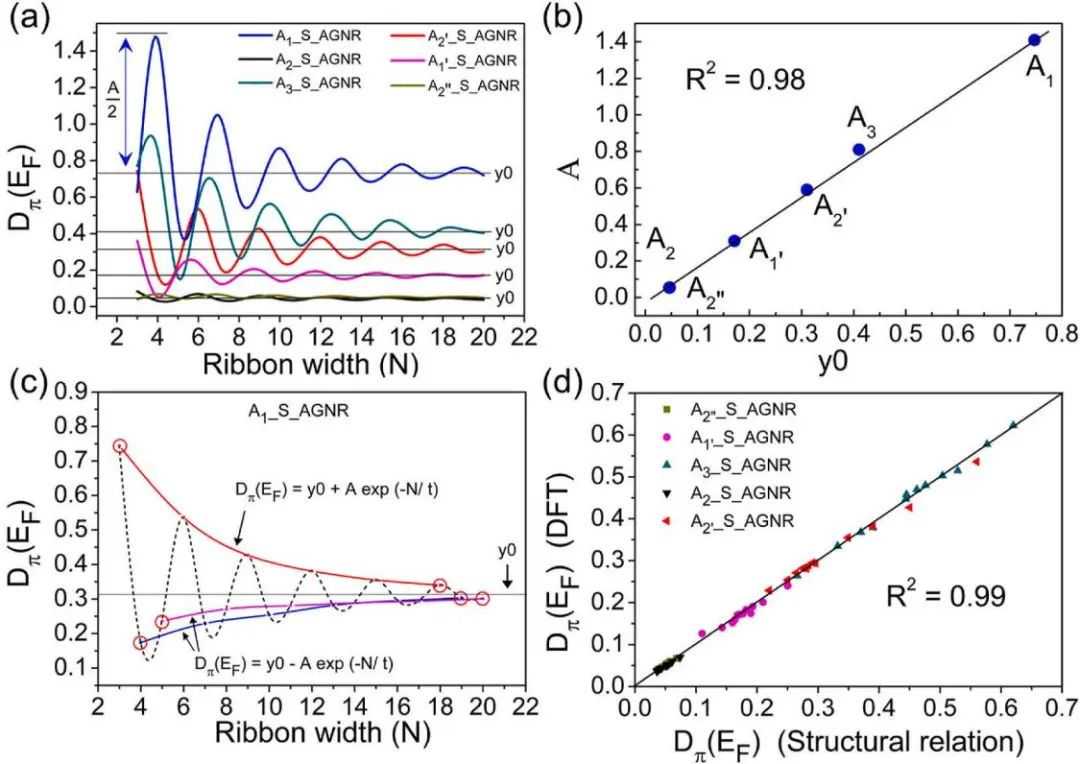
图5(a)显示6个不同活性位点的Dπ(EF)与AGNR宽度之间的关系。(b)阻尼正弦曲线振幅(A)与曲线平均值(y0)的线性相关。(c)表示对AGNR各族阻尼正弦曲线和函数的理解。红色圆圈表示DFT计算的Dπ(EF)值。(d)表示x轴上结构关系预测的Dπ(EF)与y轴上DFT计算的Dπ(EF)值
为了验证本文提出的SVR模型的预测熟练性和推广性,作者选择了不同类型的石墨烯系统,如3个氮掺杂的2D石墨烯(3NG,3NM_G,2NO_G),3个硫掺杂的1D石墨烯6-ZGNR(3S@ZGNR)和硫掺杂的0D石墨烯量子点/薄片(SGD)(图6a-e)。SVR模型的验证考虑了这些系统的少数可能的活性位点,用红色空心圈标出。研究表明,SVR算法建立的预测模型在估计任意碳位点的能量参数(ΔGOH)值时表现良好(图6f)。而预测值ΔGOH与DFT计算值的拟合优度(R2)为0.86。因此,与传统的DFT方法相比,这种QM/ML方法具有很高的成本效益和速度。最终,所提出的SVR预测模型可应用于具有不同掺杂剂/边缘/异质结构/缺陷的石墨烯体系的快速筛选,以发现ORR碳催化剂中的活性构型。
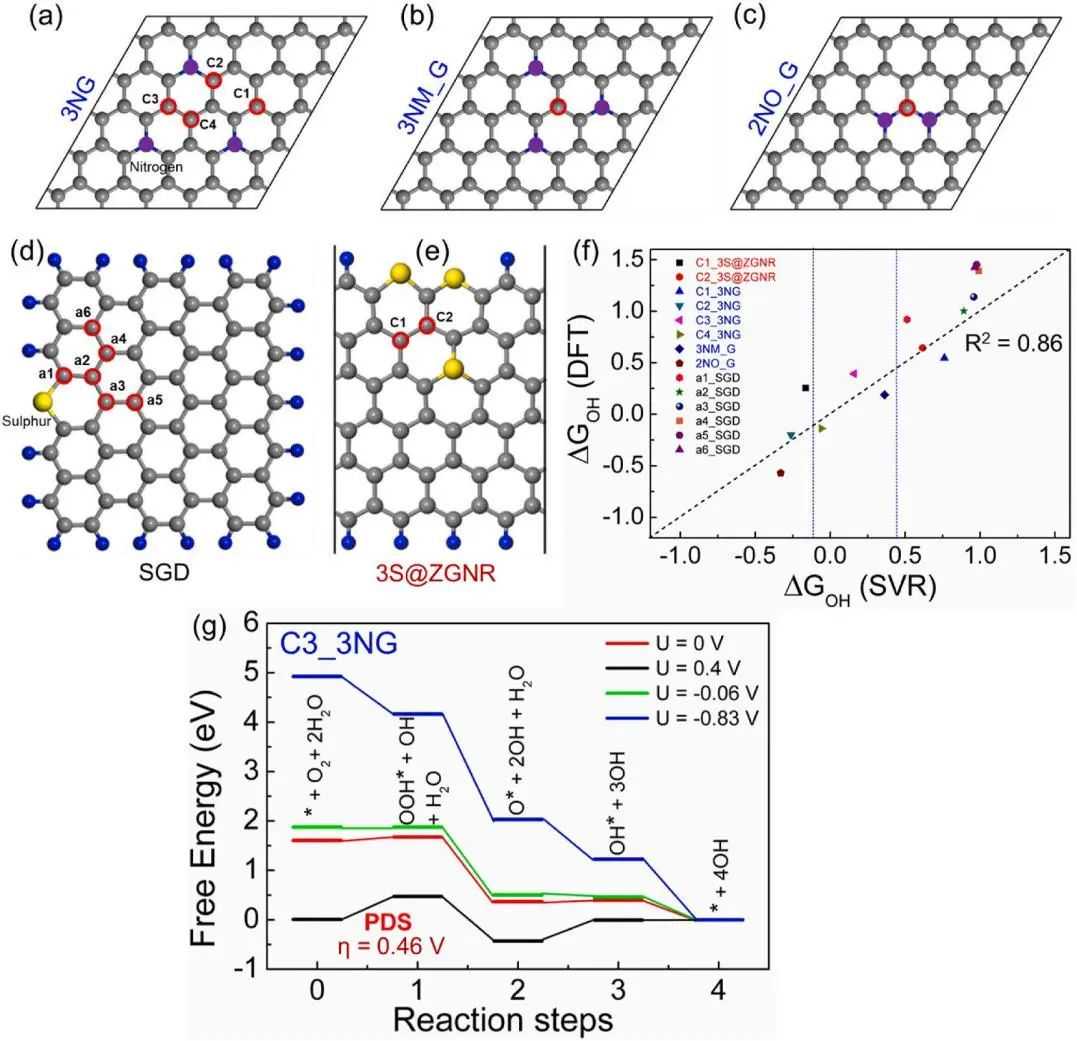
图6碳基材料应用SVR方式的拓展筛选
结论与展望
本文通过DFT研究揭示了π轨道描述子(Dπ(EF),R-Oπ)在ORR碳基催化剂活性中的重要作用,采用MLR、DTR、RFR、KNN、SVR和XGBoost六种机器学习算法,建立ΔGOH的预测模型。其中,SVR预测模型发现更有效,与DFT计算ΔGOH数值之间有着良好的拟合优度(R2=0.87)。拓展到(0D,1D,2D)掺杂石墨烯体系依旧存在这良好的ML筛选规律,这种具有成本效益的QM/ML方法可以有效的实现快速研发有前途的ORR碳基电催化剂,并扩展到各种反应中。
文献信息
Kapse,S.,Barman,N.,Thapa,R.(2023).IdentificationofORRactivityofrandomgraphene-,201,703-711.ht+tps:///10.1016/